Andreas Moshovos
Spring 2008, Updated 2012, Fall 2024
Subroutines
Structured programming relies on subroutines. Restricting our attention to C, we could write a subroutine that accepts three numerical arguments and returns their sum. This subroutine can then be used (or called) from many different places in our program. That is we could for example write the following in C:
int add3 (int a, int b, int c){
return a + b + c;
}
int sum = 0;
main () {
sum += add3 (1, 2, 3);
sum += 10;
sum += add3 (10, 20, 30);
}
For C subroutines to work as intended we need the following functionality:
· We should be able to call a subroutine from anywhere in our program. By “call” we mean being able to change control flow so that the routine is executed.
· We should be able to pass parameters that may take different values across different calls.
· A subroutine must be able to return a value.
· A subroutine must be able to change control flow so that execution continues immediately after the point where it was called. Since a subroutine can be called from many different places this suggests that the routine should be able to differentiate between them and “return” to the right spot depending on where it was called from.
We can see these requirements at work in our example:
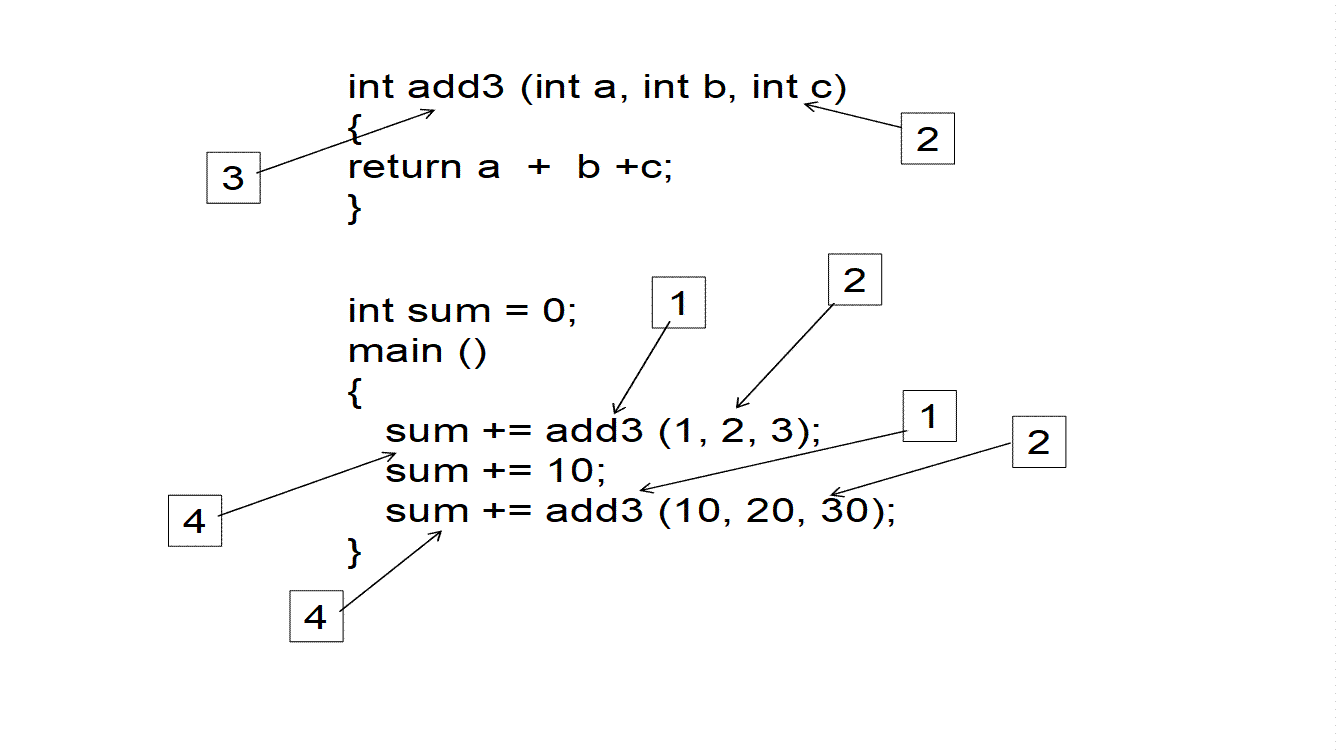
We can see that the add3 subroutine is called from two different places. The place a routine is called from is also referred to as a call site. The three parameters that add3 accepts take different values at each call site ((1,2,3) and (10,20,30)). Add3 “returns” a value which is the sum of its three arguments. So, every time add3 is called, it calculates a result and that result is returned as the subroutine’s value. This value can then be used in an expression (e.g., in add3(10,20,30) evaluates to 60). The first time add3 is called we expect execution to resume immediately after the statement that called it. So, once add3(1,2,3) returns execution will resume by adding the return value to sum. Then, the “sum += 10” statement will get executed. The second time add3 is called execution resumes immediately after the particular call.
Let’s review the way control flows in time with subroutines with aid of the add3 example:
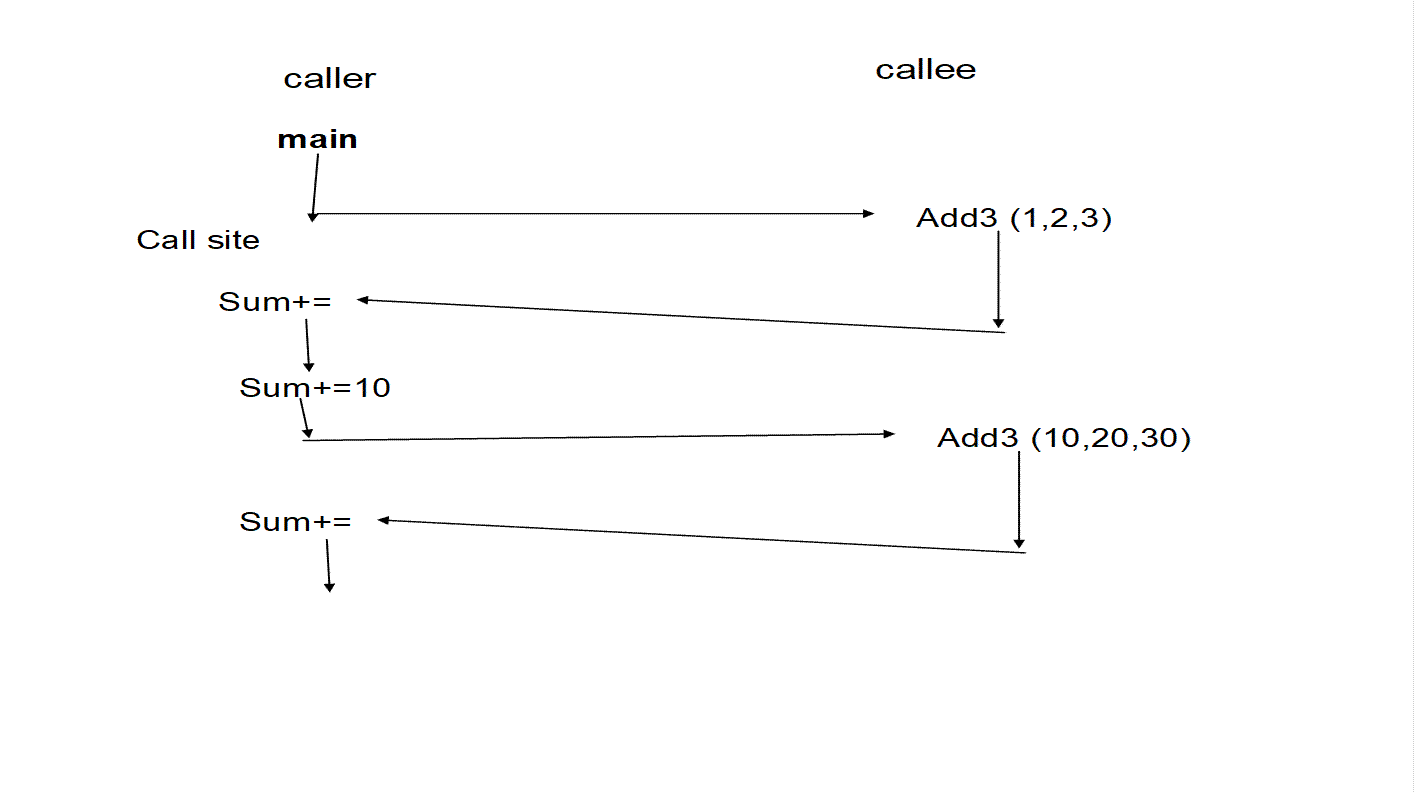
This diagram also shows a call site, the caller and the callee. The call site is the place a subroutine is called. The caller is the subroutine that is making the call. The callee is the subroutine that is called.
We can now look at the list of required functionalities and since we are interested in how to implement subroutines in assembly we can add concerns/requirements that related to machine level constructs. Thus we need to provide answers for the following questions:
· How does the subroutine returns immediately after the call site?
· Where and how does it return a value?
· Where and how are we passing arguments to a subroutine?
· Where and how are we allocating storage for any local variables (i.e., variable that belong to the subroutine)
· What happens to register values once a subroutine is called. Do we require that the subroutine preserves their values or is it OK to overwrite some registers.
We will address each of these issues in turn. For most machines there is a set of rules that all valid subroutines must follow. This set of rules is called the calling convention. This set of rules is not the only viable option for implementing subroutines. However, at some point someone decided on a particular solution. If we want a subroutine to interoperate correctly with other subroutines (possibly written by others) we have to follow these set of rules. This way someone else could also use our subroutines. We will be describing the calling convention used by gcc (for the linux operating system) for the NIOS V family of processors. There are other conventions in use in NIOS V. At any given point of time one of them can be in use, or special code must be devised to translate from one form to the other (and we do not want that).
There are a few different options for providing the aforementioned functionality. We will present the solution used in NIOS V and once this is understood we will discuss some of the other options. Key to supporting subroutines in NIOS V is the use of a stack. This stack is used to provide the functionality explained in points 1 through 5 above. We first explain how a stack can be implemented in NIOS II machine code and then explain how the stack is used to support subroutines.
STACK:
Let’s review what stack is. Stack is a last-in first-out (LIFO) queue. In more detail, the stack is a data structure for which three operations are defined:
- Push value
- Pop
- Top (distance)
The first operation adds a new element onto the stack. The order in which elements are added onto the stack is important. Internally, the elements are placed in a queue following exactly the order in which they were inserted. Push takes a single argument which is the value we will insert onto the stack. After a push, the number of stack elements increases by one. The pop operation removes the most recently inserted element within the stack. After a pop, the number of items in the stack is reduced by one. If the stack is empty then pop is not a valid operation.
Top returns the value of a stack element without removing it from the stack. Top accepts a single argument which specifies the relative to the most recently inserted element of the element we are interested in. So, top(0) returns the value of the most recently inserted element (this is also called the top of the stack , which corresponds to viewing the stack as a vertical queue with elements being placed on top of each other). Top(3) returns the value of the 4th element in the stack (as measured starting from the top).
For example, assuming that initially the stack is empty here’s an example of how the stack operates:
- Push 3 à (3)
- Push 4 à (4,3) , where 4 is the top element
- Push 10 à (10, 4, 3)
- Top(2) à returns 3
- Top(1) à returns 4
- Pop à returns 10 and then the stack becomes (4, 3)
The NIOS V STACK:
By convention the NIOS V uses a stack to support subroutines (the stack is also used to support interrupts and in other machines to support OS calls). The stack is implemented in memory with register x2 (alias “sp”) pointing to the top of the stack. That is, sp contains a value which corresponds to the address of the top element of the stack in memory. The NIOS V stack (very much like most stacks for other CPU families) grows towards lower addresses. The exact value the stack takes typically depends on the machine and the operating system running. On the CPULATOR, there is an initialization code that sets the stack to be at 0x0400000 when your code is called. This initialization code makes a call to your main() function. In older UNIX-based systems (linux is one) this code is in file crt0.o which is linked with your program. In most machines and OSes today a program is laid out in memory so that the program instructions appear first. Then follows the statically defined data (global variables), and then comes the heap (see note below) which grows towards higher addresses. At the very end of memory starts the stack and grows downwards. On the CPULATOR a program is laid out as follows:
|
0x10000 |
Instructions (.text section) |
|
|
Statically defined data (global variables in C) (.data and .bss sections) |
|
|
|
|
|
|
|
0x400000 |
Stack: |
Empty Stack? In NIOS V there is no way to represent an empty stack. The sp always has a value and this always corresponds to a valid address (they are both 32 bit numbers). If you do use sp to read from memory you will read the element at the top of the stack. If you did not push an element, you are just reading the value that happens to be there where sp points to. It would be garbage for all we care but you will still be able to read a value. So, whether the stack is empty and how elements it holds is a concept that only the programmer can understand and its all a matter of convention and of using the appropriate operations in sequence to achieve the effect we desire.
What’s in the stack? On another related note, an element in memory is within the stack if its address is equal to or higher than the value of sp. Finally, we can use sp instead of x2. “sp” is an alias for “x2”.
(*) the heap is used for dynamic memory allocation in several programming languages. For example, in C when you use malloc() this is where the memory comes from. Similarly, in C++ you use “new” to get memory in the heap. In Java, objects are allocated within the heap. There is no need for hardware support for the heap. It’s all done with appropriate manipulation of register or memory variables. That is, the heap is a software construct. But for our purposes we can safely ignore this topic for the time being.
PUSH value: Here’s how push can be implemented in NIOS V assembly. Let’s assumed that the value we want to push onto the stack is in register x10:
addi sp, sp, -4 à grow the stack by four bytes (a word)
sw x10, 0(sp) à save the value of x10 onto the top of the stack
POP: Let’s assume that in addition to removing an element from the top of the stack pop also returns its value into register x10.
1. lw x10, 0(sp) à read top value
2. addi sp, sp, 4 à increment the stack pointer thus removing the top element
Top (index): Assuming that all elements in the stack are words then we could access the ith element using a sequence of instructions. For example, if we assume that i (our index) is in register x10, then we can use:
add x10, x10, x10 à assume x10 holds i
add x10, x10, x10 à x10 = 4 * i
add x10, sp, x10 à the address of the element in the stack is sp + 4*i
lw x10, 0(x10) à return value of the ith element into x10
If “i” is not a variable but a constant we can use just a load to read the value from the stack. For example:
lw x10, 16(sp)
reads the fourth element of the stack assuming that all elements are words.
To avoid writing too long hexademical numbers in the example that follows we assume that the stack started at 0x70000. Let’s assume that the stack has the following values (all values in hexadecimal):
|
SP --> 0x6fff0 |
01 |
02 |
03 |
04 |
|
0x6fff4 |
10 |
20 |
30 |
40 |
|
0x6fff8 |
11 |
22 |
33 |
44 |
|
0x6fffc |
55 |
66 |
77 |
88 |
Here are a few examples:
lw x10, 8(x10) à x10 = mem[sp + 8] = mem[0x6fff0 + 8] = mem[0x6fff8] = 0x144332211
lb x11, 0xd(sp) à x11 = mem[sp + 0xd] = 0x66 (this reads a single byte and sign extends it into 32 prior to writing into x11).
Requirement 1: Calling a subroutine and having it return to the caller
Having explained the stack we are now ready to explain how the first requirement can be satisfied using the stack. Let’s focus only on control flow for the time being and thus use subroutines that do not accept arguments and do not return values. Let’s use the following C code as our example:
boo () {
coo ();
}
coo () {
return;
}
In this example function boo calls function coo. Here’s the assembly code:
.text
boo:
call coo
…
coo:
ret
There are two new instructions: “call coo” and “ret”. “Call coo” does:
x1 = PC + 4
PC = coo
where x1 can also be referred to as “ra” for “return address”.
The “ret” instruction does:
PC = x1
Note: The “call” and “ret” instructions are aliases and are implemented using other RISC V instructions. They each map to one instruction, we will defer the discussion on what are the actual instructions for later one. Using “call” and “ret” is convenient and makes our programs more readable and manageable and since each maps to one instruction we will keep using them as such.
Back to calling and returning: So, boo(), prior to calling coo(), saves in register x1 (alias “ra”), the address of the instruction that it wants coo() to return to. This address is the address of the call plus four since every instruction is four bytes long. When coo returns, it simply uses “ret”.
The aforementioned example works without needing a stack because we have only one call. Let’s see what happens if coo() were to make a few calls also. Let’s look at the following code:
boo_calls (){
coo ();
doo ();
return;
}
void coo (){
doo ();
return;
}
void doo(){
return;
}
A function that gets called from two different places (call sites): Notice that boo() calls coo() which then calls doo(). After doo() returns to coo() and it returns to boo(), boo() calls doo() directly. Still here? Focusing thus on doo(), we see an example where a function is called from two different places and is supposed to return at different spots for each of those calls.
The “trick” is to apply the following convention: If a function will be calling another it has to save the ra value on the stack in the beginning and restore it from the stack prior to returning. Here’s the code:
The NIOS C code is as follows:
.text
boo: # boo will be making calls, so it first pushes the ra value on the stack
addi sp, sp, -4
sw ra,0(sp) # push the return address onto the stack
call coo # resume execution at coo, ra = PC + 4 = boo_ret1
boo_ret1:
call doo # continue execution at doo, ra = PC + 4 = boo_ret2
boo_ret2:
lw ra, 0(sp) # pop return address from the stack
addi sp, sp, 4
ret # resume execution there
coo:
addi sp, sp, -4
sw ra,0(sp) # push the return address onto the stack
call doo # resume execution at coo, ra = PC + 4 = coo_ret
coo_ret:
lw ra, 0(sp) # pop return address of boo from the stack
addi sp, sp, 4
ret # resume execution there
doo: # doo will not be making any calls, no need to save ra on the stack
ret # just return to whoever called
The first two instructions push on the stack the return address for the call to coo. The return address is the address of the instruction that follows the call in the calling function. We use the label “boo_ret1” to refer to this address which is the PC of the “call coo” plus 4.
addi sp, sp, -4 à make space on the stack for a word
sw ra, 0(sp) à save return address for boo onto stack
call coo à ra = PC + 4, PC = coo, continue execution at coo
after these instructions have been executed, the PC points to “coo” and the stack contains a single word element whose value is the address of the instruction that boo should return to eventually. In coo now, the first two instructions push onto the stack the return address for coo, which in this case is boo_ret1; when coo returns execution should continue immediately after the “call coo”. So, at this stage, the stack contains two words. At the top of the stack is the return address for coo. After it is the return address for boo.
Leaf Functions: Since doo does not call any other routines, it does not need to save the “ra” on the stack. It can simply return to whoever called it. To do this, “doo” uses a “ret” to resume execution at that address. Function doo is a “leaf function”, meaning it does not call any other functions.
Once doo returns, the PC will point to coo_ret. The instruction sequence starting at coo_ret pops the saved return address for coo and then returns to it. Specifically:
lw ra, 0(sp) à restore ra from the stack, ra becomes boo_ret1.
add sp, sp, 4 à adjust the stack (value popped)
ret à return to boo at address boo_ret
Back in boo, we then call doo. This changes the PC to point to doo while ra becomes boo_ret2 which is the address of the “call doo” plus four. Doo again uses ra to return to whoever called it. After doo returns, we go to boo_ret1. Finally, boo pops the saved return value from the stack and returns to whichever function called it.
Notice that while the first time doo was called the return address was pointing in coo, during the second call to doo the return is in boo. Also note that while boo called coo, coo was able to call doo. The stack thus allowed us to implement nested calls and have each one of them return appropriately.
Here’s how the code looks like in memory when compiled on the CPULATOR:

In the code “jal” is the instruction implementing “call”. More on this later on. For the time being treat “jal” as “call”.
Here’s how the code executes step-by-step on CPULATOR. In this example, we assume that when boo is called ra holds the value 0x100d8, this is the return address for boo(). We also assume that the stack initially points to 0x20 000c. The values used when executing the code on the lab’s boards may be different. This does not matter, the point is that as long as the stack does not overflow into .data or .text the code will work independently of where the stack actually is.
See powerpoint slides.
Implementation of “call” and “ret”
“call” and “ret” are pseudo-instructions supported by the assembler. They are implemented using “jal” or “jalr”. Let’s first describe “jal”. “jal” stands for “Jump and Link”. It takes the form:
jal xX, label
Where xX a register. It does:
xX = PC + 4, PC = label
The instruction first saves into xX the address of the next instruction in memory (PC+4) and then continues execution at the address identified by “label”. “call” is using x1 (ra):
call label à jal ra, label à jal label (assembly alias)
The target address in “jal” is given as an offset from the current PC. The offset is a signed 21b immediate and thus “jal” can be used when the label is at most +/- 1MB away from the “jal”:
![]()
If we wish to call a function that is further away we can use “jalr” which stands for “jump and link register” where the target address is given by another register operand:
jalr xY, xX, imm à
xX = PC + 4 (e.g., xX = ra)
PC = xY + sign-extend(imm) / imm is 12b
“Jalr” stores in xX (typically “ra”) the address of the next instruction (PC+4). This is identical to “jal”. The difference is in how it calculates the target address. For that it uses the value stored in the second register operand xY adding an immediate of 12b (signed).
![]()
“Jalr” uses the same encoding format as loads or stores and the assembler also supports an alternate syntax that looks like a load or a store. For example:
Jalr x10, ra, 0 is the same as jalr ra, 0(x10)
I don’t like this alternate syntax since it may create the impression that the instruction accesses memory at the address x10+0. It does not perform a memory read or write. It uses the value of register x10, add the offset (0 in this case) and then jumps to the address (PC = x10+0).
Implementation of “ret”: “ret” is implemented as:
ret è jalr x0, ra, 0
As described, this does:
x0 = PC + 4 (discarded since x0 is always 0)
PC = ra + 0 = ra